OpenMP vs POSIX threads
Both are APIs for shared-memory programming. In C, OpenMP is a relatively high-level extension, providing compiler directives for parallelizing many programs with ease while some low-level thread interactions may be difficult to program. Pthreads provide some low-level coordination constructs that are unavailable in OpenMP, making other programs easier to parallelize while requiring explicit specification of the behavior of each thread, which may virtually be any that is conceivable.
Pthreads programs can be used with any C compiler, provided the system has a Pthreads library. OpenMP requires compiler support for some operations, which many compilers provide.
Area Under the Curve
The program we are about to develop is oftentimes called the 'Hello world!' of parallel programming. We will be using the following formula for arctan(1)1 in approximating the value for π.
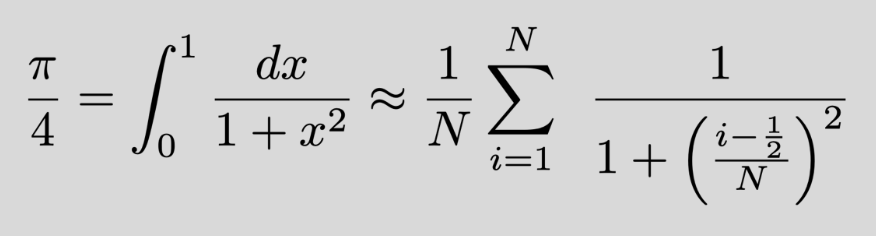Just as we learned a long time ago in Kindergarten, the value of the integral here is the area between the graph and the x-axis while x goes from 0 to 1.
Going through the serial version of the program in C, the value for above is calculated for each integer within range [1, N) and summed up within a loop. The resulting sum is them divided by N for getting an estimate of π / 4, before printing out the calculated approximate for π.
#include <stdio.h>
#include <sys/time.h>
#include <unistd.h>
#include <math.h>
int main() {
unsigned int N=999999999;
long double sum=0, quarter_of_pi=0;
for (unsigned int i=1; i <= N; i++) {
sum += 1 / ( 1 + (long double) pow(( i - 0.5 ) / N, 2) );
}
quarter_of_pi = sum / N;
printf("Time taken: %.3lf seconds\n", tcalc);
printf("Quarter of Pi ~ %.15LF\n", quarter_of_pi);
printf("Pi ~ %.15LF\n", quarter_of_pi * 4.0);
return 0;
}A parallel version of the above code is shown below. Notice the directives for compiler, starting with #pragma, and the inclusion of omp.h header.
#include <omp.h>
#include <stdio.h>
#include <unistd.h>
#include <math.h>
int main() {
unsigned int N=999999999;
long double sum=0, quarter_of_pi=0;
double tstart, tcalc, tstop;
tstart = omp_get_wtime();
sum = 0;
omp_set_num_threads(24)
#pragma omp parallel
{
double sum_thread=0; // local to each thread
#pragma omp for
for (unsigned int i=1; i <= N; i++) {
sum_thread += 1.0 / ( 1 + (long double) pow(( i - 0.5 ) / N, 2) );
}
#pragma omp atomic
sum += sum_thread;
}
quarter_of_pi = sum / N;
tstop = omp_get_wtime();
tcalc = tstop - tstart;
printf("Time taken: %.3lf seconds\n", tcalc);
printf("Quarter of Pi ~ %.15LF\n", quarter_of_pi);
printf("Pi ~ %.15LF\n", quarter_of_pi * 4.0);
return 0;
}To compile above with gcc, use following.
gcc -o <outputname> <filename>.c -f openmp -lm -Wall -g
Modifying Parallelized Code
Before changing anything, it pays to understand whatever we want changed in the first-place. So, let us go through the above code. The function omp_get_wtime(), defined in omp.h, returns the amount of seconds since a previous fixed point in time (included for execution timing purposes). Setting the number of threads to spawn when running parallel code (code inside parallel scope, that is) done by omp_set_num_threds. Changing the set to get and calling from within a parallel section returns the number of threads in execution (get counterpart is available for most functions with set). However, due to resource constraints on the system, it is possible we ending up with a lower number of threads.
The directive #pragma omp parallel is for parallelizing the code–it is safe to assume if this is not present somewhere, the program will not be parallelized by OpenMP. The scope of code that needs to be executed in parallel may be defined the same way we do scoping in C, with {}, or without–whereas only immediately following code line will be considered in-scope. This is where new threads will be spawned and start running alongside the master thread, branching the execution.
Any variables created within the parallel scope are private for each thread (i.e. sum_thread), and will not contribute to race conditions. Therefore, the for loop incrementing sum_thread is divided among threads spawned. Please note the way threads divide the iterations among themselves can be handled up to some extent with specific directives, the default behavior is expected here by omitting them.
Critical sections may be scoped within #pragma omp atomic or #pragma omp critical. The former enables low level atomicity of execution (with higher performance) if available, and only accepts a single assignment statement (of an allowed form) within scope, while the latter can handle multiple statements. Both effectively serializes execution. If we end up with most of the code within the scope of either, our code is probably too poor for parallelization with OpenMP.
Outside the #pragma omp parallel scope, previously spawned threads will join the master thread, and it will continue executing similar to a serial program. It is worth mentioning that we may have as many parallel/serial sections as we please.
As should be apparent from above, OpenMP is designed to be easy to learn and can be used for parallelizing existing serial code with minimal modifications. What if we could further simplify the above code?
Reducing the Parallel Code
Modifying the sum variable at the end of the for loop in above code could be simplified with a reduction operation provided by OpenMP. That is, we can instruct OpenMP to synchronously add the local sum calculated by each thread (within loop) to the shared variable sum as shown in the parallel version below.
#include <omp.h>
#include <stdio.h>
#include <unistd.h>
#include <math.h>
int main() {
unsigned int N=999999999;
long double sum=0, quarter_of_pi=0;
double tstart, tcalc, tstop;
tstart = omp_get_wtime();
sum = 0;
omp_set_num_threads(24);
#pragma omp parallel for reduction(+:sum) shared (N)
for (unsigned int i=1; i <= N; i++)
sum += 1.0 / ( 1 + (long double) pow(( i - 0.5 ) / N, 2) );
quarter_of_pi = sum / N;
tstop = omp_get_wtime();
tcalc = tstop - tstart;
printf("Time taken: %.3lf seconds\n", tcalc);
printf("Quarter of Pi ~ %.15LF\n", quarter_of_pi);
printf("Pi ~ %.15LF\n", quarter_of_pi * 4.0);
return 0;
}Here, we have a single statement #pragma omp parallel for that tells we want the immediately-following for loop parallelized, which is identical to having #pragma omp for immediately before a for loop within the scope of #pragma omp parallel. The reduction(+:sum) tells that we want the sum variable to contain the sum of each local sum calculated in each iteration only available locally to the thread that runs it. OpenMP does this by creating a private sum variable for each thread and initializing it to unit according to the operation (ex. 0 for +, 1 for *), this is how we use the reduction operator in OpenMP. The shared(N) tells that the N variable should be shared with all threads, this is fine since threads are only reading it–therefore no potential data races. Finally, the approximated values along with the time taken for calculations are printed.
Now that we went through the code, note that the omp_set_num_threads is not mandatory when using OpenMP, the program defaults to spawning the maximum number of threads possible on the system at execution time. Timing information for serial and parallel (24 threads) versions resulted2 in ~9.75 and ~0.76 seconds respectively: speedup3 ~13.